segunda-feira, 28 de fevereiro de 2011
sexta-feira, 25 de fevereiro de 2011
Tipos de decimais.
Decimais
Decimais exatos
 =
= 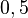
 =
= 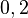
Decimais periódicos
 =
=  (a)
(a) =
=  (b)
(b)Os decimais periódicos são denominados dízimas periódicas. As dízimas periódicas podem ser simples como no exemplo (a) ou compostas como no exemplo (b). A fração que originou a dízima periódica é denominada de fração geratriz e a parte que repete na dízima é denominada período.
Tipos de frações.
Tipos de frações
- própria: o numerador é menor que o denominador. Ex.:

- imprópria: o numerador é maior que o denominador. Ex.:

- mista: constituída por uma parte inteira e uma fracionária. Ex.:
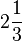
- aparente: o numerador é múltiplo do denominador. Ex.:

- equivalentes: aquelas que mantêm a mesma proporção de outra fração. Ex.:

- irredutível: o numerador e o denominador são primos entre si, não permitindo simplificação. Ex.:

- unitária: o numerador é igual a 1 e o denominador é um inteiro positivo. Ex.:

- egípcia: fração que é a soma de frações unitárias, distintas entre si. Ex:
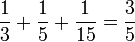
- decimal: o denominador é uma potência de 10. Ex.:

- composta: fração cujo numerador e denominador são frações:
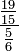
- contínua: fração constituída a partir de uma sequência de inteiros naturais (a0,a1,a2,a3,...,ak,...) da seguinte maneira

- Quando esta fração contínua termina, o seu resultado é um número racional, porém quando esta fração não termina, o resultado pode ser racional ou irracional.
Exercício com frações e decimais.
1. Qual é a alternativa que representa a fração 9/2 em números decimais?
a. 3,333
b. 4,25
c. 5,01
d. 4,5
2. Qual é a alternativa que representa a fração 35/1000 em números decimais?
a. 0,35
b. 3,5
c. 0,035
d. 35
3. Qual é a alternativa que representa o número 0,65 na forma de fração?
a. 65/10
b. 65/100
c. 65/1000
d. 65/10000
4. Observe as frações e suas respectivas representações decimais.
I. 3/1000 = 0,003
II. 2367/100 = 23,67
III. 129/10000 = 0,0129
IV. 267/10 = 2,67
quinta-feira, 24 de fevereiro de 2011
Não se esqueça!
Racionais em: Positivos,Negativos e Escrita Fracionaria
Racionais Positivos e Racionais Negativos
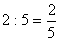
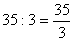
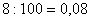
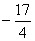 é um número racional negativo
é um número racional negativo 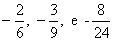 têm valor igual a
têm valor igual a 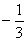 e representam o número racional
e representam o número racional 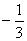 .
. 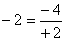 Denominamos número racional o quociente de dois números inteiros (divisor diiferente de zero), ou seja, todo número que pode ser colocado na forma fracionária, em que o numerador e denominador são números inteiros.
Denominamos número racional o quociente de dois números inteiros (divisor diiferente de zero), ou seja, todo número que pode ser colocado na forma fracionária, em que o numerador e denominador são números inteiros.
Racionais Positivos e Racionais Negativos
O quociente de muitas divisões entre números naturais é um número racional absoluto.
Números racionais positivos e números racionais negativos que sejam quocientes de dois negativos que sejam quocientes de dois números inteiros, com divisor diferente de zero.
Por exemplo:
(+17) : (-4) = 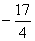
Números Racionais Positivos
Esses números são quocientes de dois números inteiros com sinais iguais.
· (+8) : (+5) 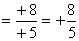
· (-3) : (-5) 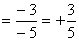
Números Racionais Negativos
São quocientes de dois números inteiros com sinais diferentes.
· (-8) : (+5) 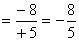
· (-3) : (+5) 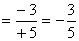
Números Racionais: Escrita Fracionária
Obs.: Todo número inteiro é um número racional, pois pode ser escrito na forma fracionária:
quarta-feira, 23 de fevereiro de 2011
Matemático dos números racionais.
George Ferdinand Ludwig Philipp Cantor |
Em 1872 Cantor foi promovido a professor Extraordinário em Halle e neste ano tornou-se amigo de Dedekind que ele conheceu num feriado passado na Suíça. Cantor publicou um artigo sobre séries trigonométricas em 1872 na qual ele define um número irracional em termos de seqüências convergentes de números racionais. Por outro lado, neste mesmo ano, Dedekind publicou sua definição de números reais como "cortes de Dedekind" e no seu artigo ele faz referência ao artigo que tinha recebido de Cantor.
Em 1873 Cantor provou que o conjunto dos racionais é contável, isto é, que pode ser posto em correspondência um para um com os números naturais. Ele também mostrou que os números algébricos, números que são raízes de equações polinomiais com coeficientes inteiros, também são contáveis. No entanto sua tentativa para provar que os reais eram contáveis se mostrou um pouco mais difícil. Ele provou que os números reais não eram contáveis em dezembro de 1873 e publicou isto num artigo de 1874. Neste artigo a idéia de uma correspondência um para um aparece pela primeira vez, mas somente implícita no trabalho.segunda-feira, 21 de fevereiro de 2011
O que são números racionais?
http://24hmatematica.blogspot.com/2009/09/afinal-para-que-serve-matematica.html
São aqueles que podemos escrever na forma de fração entre números inteiros, com o denominador diferente de zero. São exemplos: 0,05 (um decimal exato), que pode ser obtido pela divisão entre 5 e 100, ou seja, pode ser escrito como 5/100; -43 e 12 (números inteiros), que podem ser escritos como -43/1 e 12/1; a dízima periódica 0,33333..., que pode ser escrita como o resultado da divisão entre 1 e 3, então 1/3. A fração representa uma razão entre duas grandezas, isto é, uma comparação entre medidas do mesmo tipo. Assim, com os números racionais, podemos medir e resolver problemas de proporcionalidade, porcentagem e probabilidade, por exemplo.
Conjunto dos Números Racionais
Conjunto dos Números Racionais
Os números racionais surgiram da necessidade de representar partes de um inteiro. Durante as inundações do Rio Nilo, no Egito Antigo, as terras que ficavam submersas recebiam muitos nutrientes, dessa forma tornavam-se muito férteis para a agricultura. Quando as águas baixavam, era necessário remarcar os limites entre os lotes de cada proprietário. Por mais eficiente que fosse a medida utilizada, dificilmente ela caberia um número inteiro de vezes na corda, isso levava a utilização das frações.
O conjunto dos números racionais engloba todos os algarismos na forma de a/b, com b ≠ 0, isto é, os números fracionários e as dízimas periódicas (números decimais). O conjunto é representado pela letra Q maiúscula. Observe alguns exemplos de números racionais:
3/5 ou 0,6
4/9 ou 0,4444...
2/11 ou 0,18181818...
1/3 ou 0,33333...
–36/10 ou –3,6

Observações importantes sobre os números racionais.
1º – Todo número inteiro é um número racional. Exemplos:
0 = 0/1 – 6 = – 6/1 2250 = 2250/1 – 500 = –500/1
2º – Todo número decimal exato é um número racional. Exemplos:
7,6 = 76/10 0,5 = 1/2 – 12,8 = 128/10 6,32 = 632/100
3º – Toda dízima periódica é um número racional. Exemplos:
0,444444... = 4/9 0,33333... = 1/3 0,6777777.... = 61/90 –0,344444... = –31/90
Todo número inteiro é um número racional, portanto, o conjunto dos números inteiros (Z) é um subconjunto do conjunto dos números racionais (Q). Veja demonstração através da utilização de diagramas:
Q* = conjunto dos números racionais com ausência do zero.
Q+ = engloba somente os números racionais positivos.
Q– = engloba somente os números racionais negativos.
Q*+ = engloba somente os números racionais positivos com ausência do zero.
Q*– = engloba somente os números racionais negativos com ausência do zero.
Os números racionais surgiram da necessidade de representar partes de um inteiro. Durante as inundações do Rio Nilo, no Egito Antigo, as terras que ficavam submersas recebiam muitos nutrientes, dessa forma tornavam-se muito férteis para a agricultura. Quando as águas baixavam, era necessário remarcar os limites entre os lotes de cada proprietário. Por mais eficiente que fosse a medida utilizada, dificilmente ela caberia um número inteiro de vezes na corda, isso levava a utilização das frações.
O conjunto dos números racionais engloba todos os algarismos na forma de a/b, com b ≠ 0, isto é, os números fracionários e as dízimas periódicas (números decimais). O conjunto é representado pela letra Q maiúscula. Observe alguns exemplos de números racionais:
3/5 ou 0,6
4/9 ou 0,4444...
2/11 ou 0,18181818...
1/3 ou 0,33333...
–36/10 ou –3,6
Observações importantes sobre os números racionais.
1º – Todo número inteiro é um número racional. Exemplos:
0 = 0/1 – 6 = – 6/1 2250 = 2250/1 – 500 = –500/1
2º – Todo número decimal exato é um número racional. Exemplos:
7,6 = 76/10 0,5 = 1/2 – 12,8 = 128/10 6,32 = 632/100
3º – Toda dízima periódica é um número racional. Exemplos:
0,444444... = 4/9 0,33333... = 1/3 0,6777777.... = 61/90 –0,344444... = –31/90
Todo número inteiro é um número racional, portanto, o conjunto dos números inteiros (Z) é um subconjunto do conjunto dos números racionais (Q). Veja demonstração através da utilização de diagramas:
Dentro do conjunto dos números existem os seguintes subconjuntos:
Q* = conjunto dos números racionais com ausência do zero.
Q+ = engloba somente os números racionais positivos.
Q– = engloba somente os números racionais negativos.
Q*+ = engloba somente os números racionais positivos com ausência do zero.
Q*– = engloba somente os números racionais negativos com ausência do zero.
Assinar:
Comentários (Atom)


