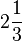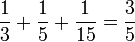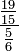Número racional é todo o número que pode ser representado por uma razão (ou fração) entre doisnúmeros inteiros.
O conjunto dos números racionais (representado por  , o uso da letra
, o uso da letra  é derivada da palavra inglesa quotient, cujo significado é quociente, já que a forma de escrever um número racional é o quociente de dois números inteiros, com o denominador diferente de 0) é definido por:
é derivada da palavra inglesa quotient, cujo significado é quociente, já que a forma de escrever um número racional é o quociente de dois números inteiros, com o denominador diferente de 0) é definido por:
 , o uso da letra
, o uso da letra  é derivada da palavra inglesa quotient, cujo significado é quociente, já que a forma de escrever um número racional é o quociente de dois números inteiros, com o denominador diferente de 0) é definido por:
é derivada da palavra inglesa quotient, cujo significado é quociente, já que a forma de escrever um número racional é o quociente de dois números inteiros, com o denominador diferente de 0) é definido por: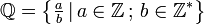 Lê-se Q igual a "a" sobre (ou dividido) "b", tal que "a" pertence ao conjunto dos numeros inteiros e "b" pertence ao conjunto dos numeros inteiros. Onde
Lê-se Q igual a "a" sobre (ou dividido) "b", tal que "a" pertence ao conjunto dos numeros inteiros e "b" pertence ao conjunto dos numeros inteiros. Onde  é o conjunto dos números inteiros e
é o conjunto dos números inteiros e  o conjunto dos números inteiros excluindo o 0.
o conjunto dos números inteiros excluindo o 0.Exemplos de números racionais:  ;
;  ;
; 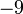 ;
; 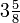 ;
; ![\,\!\sqrt[2]{4}](http://upload.wikimedia.org/math/e/a/0/ea0c7fb92d1298b193a5341ae8d140ae.png) ;
;  .
.
 ;
;  ;
; 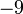 ;
; 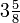 ;
; ![\,\!\sqrt[2]{4}](http://upload.wikimedia.org/math/e/a/0/ea0c7fb92d1298b193a5341ae8d140ae.png) ;
;  .
.Os números racionais opõem-se aos números irracionais ( ).
).
 ).
).Para representar o conjunto dos racionais positivos podemos usar Q + e para representar o conjunto dos números racionais negativos podemos utilizar Q-. O número zero também faz parte do conjunto dos racionais.
Há quatro formas de se apresentarem os números racionais: Frações (próprias ou impróprias),números mistos (que é uma variação das frações impróprias), números decimais de escrita finita e, por fim, as dízimas, que são números decimais em cuja escrita aparecem períodos numéricos infinitos. Eis alguns exemplos:
- Fração:
 ;
; - Número misto: 5
 ;
; - Números decimais de escrita finita: 8,35;
- Dízimas: 8,(23); 1,23(5); 7,23(965);
nesta notação os números entre parênteses repetem-se ao infinito.


 =
= 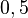
 =
= 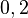
 =
=  (a)
(a) =
=  (b)
(b)